Trigonometry Flex your Muscle!

https://drive.google.com/drive/folders/17xOE9b-lJ570lQXz-EaWosB8e8Qzjw9o?usp=drive_link

Final Project Draft

 https://docs.google.com/document/d/1IFJ5MoBbvcAfM7Sa-2tdfIwXnK2VH7h_/edit?usp=drive_link&ouid=104323376055760014489&rtpof=true&sd=true

Week 9: Mathematics & traditional and contemporary practices of making and doing

Reading 

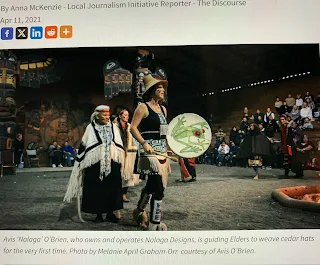
As I reflect on Avis O’Brien’s captivating journey, a Haida and Kwakwa̱ka̱ʼwakw woman weaving her way back to her cultural roots through cedar, I am struck by two significant stops in her transformative narrative.

First Stop: Reconnecting through Cedar Medicine

The initial turning point for O’Brien was in 2010 when she embraced the art of cedar weaving under the guidance of her sister, Meghann O’Brien. Before this, O’Brien harbored a sense of disconnection and shame about her identity, a product of historical impacts on Indigenous cultures. The power of cedar, described as sacred medicine, became the key that unlocked the door to her cultural heritage. This moment stands out as a powerful testament to the healing potential embedded within indigenous practices. O’Brien's experience underscores the idea that cultural reclamation can be a profound path to self-discovery and reconnection.

Second Stop: Weaving as Cultural Resilience

The historical context woven into O’Brien’s narrative reveals the deliberate suppression of Indigenous cultural practices by the Canadian government. The ban on Potlatches, a central element of First Nations' cultural and economic identity, exemplifies a systematic effort to erase indigenous cultures. As one of these suppressed practices, Weaving slept through those challenging times, but O’Brien sees its reawakening as an act of resilience. By facilitating cedar weaving workshops, she actively supports Elders in reclaiming what was taken from them throughout history. This stop on O’Brien’s journey highlights the enduring strength of Indigenous cultures and the power of individuals like her in revitalizing and preserving these traditions.

Question for Discussion:

1. In what ways does the intersection of cultural practices, such as cedar weaving, contribute to intergenerational healing and the preservation of Indigenous identity?

APTN article, Apr 11, 2021: ‘The spirit of the medicine will lead us back’: How Avis O’Brien is guiding Elders to weave their first cedar hats

Activity

This week's handmade rope-making exploration has been a delightful revelation, expanding my perspective on the mathematics embedded in a seemingly simple craft. As someone who frequently uses ropes but never considered their potential for teaching mathematics, this experience was an eye-opener. Engaging in the tactile process of creating 2-ply twine with two scarves felt like an intimate connection to a timeless human tradition, even though I quickly made the S twist and struggled with the Z twist. Sharon Kellis's insightful mention in the video of the possibility of creating a rope with anything. Also, she made the connection between rope making and the foundation of the new technology, as iPads added an extra layer of fascination to this age-old craft. Physically manipulating materials brought a profound sense of connection to our ancestors, instilling in me a grounding experience that resonates with the present.

When I made the S shape, I explored the mathematical patterning woven into each twist and turn of the scarves. It was a fascinating journey into the hidden complexities of the craft. As I twisted away from me, I marveled at the symmetry and uniformity of the resulting rope – all manifesting mathematical principles. The tension in my hands hinted at the possibility of exploring concepts like symmetry, geometry, and basic algebraic relations. It is intriguing how making rope can unveil a world of mathematical beauty, creating a bridge between the tactile and the abstract.

Indeed, handmade rope-making can be integrated into the curriculum, which opens doors to many enriching possibilities. Weaving the historical and cultural context of rope-making into lessons serves as a bridge, connecting ancient practices with contemporary mathematical understanding. For instance, students can be introduced to the mathematical concepts of symmetry, geometry, and algebraic relations through hands-on activities that bring these principles to life and engage students in a multisensory learning experience. Emphasizing the tactile sensation of rope making, the visual observation of patterns, and the kinesthetic experience of twisting creates holistic learning styles, making mathematical concepts more accessible and engaging.

In summary, handmade rope-making emerges as a powerful interdisciplinary tool, seamlessly weaving together history, culture, and mathematics. As educators, incorporating this craft into our teaching practices provides students with a unique and immersive learning experience, fostering a deep appreciation for the mathematical principles at play and the cultural significance of traditional crafts. As I reflect on this exploration, I am left wondering what unique perspectives students might bring to this age-old craft and how it could become a gateway for them to appreciate the mathematical and cultural significance of hands-on learning.

Top of Form

 

1) The art and geometry of rope making and yarn plying

2) Weaving the Bridge at Q’eswachaka

 

Week 8: Mathematics & fibre arts, fashion arts and culinary arts

 

Reflection on the Reading:

Exploring Ratios and Sequences with Mathematically Layered Beverages by Andrea Johanna Hawksley

As I delved into Andrea Johanna Hawksley's exploration of teaching ratios and sequences through layered beverages, I was captivated by the innovative approach to blending math with culinary delight. Two prominent stops in this reading stood out to me, offering unique insights into the intersection of mathematics and food.

The first notable stop is the introduction of simple two-layered beverages, a clever tool to enhance comfort with fractions and ratios. The author seamlessly integrates mathematics into cooking, highlighting the strict ratios in recipes and emphasizing the importance of understanding fractions. The example of expressing sweetness as a ratio between layers—3:5, for instance—creates a tangible link between the abstract world of numbers and the delicious experience of consuming layered drinks.

The second stop takes me into exploring sequences using beverages with many layers. The limitation that each layer must be less dense than the previous one narrows down the feasible sequences, introducing a fascinating challenge. The author introduces sequences like the Fibonacci sequence, demonstrating how the layers' proportions can mirror the sequence's mathematical properties. Creating a Fibonacci lemonade, where the intensity of flavors increases exponentially, adds a delightful twist to the exploration.

These stops underscore the dynamic relationship between mathematics and the sensory experience of consuming layered beverages. The interactive nature of the workshop engages participants in hands-on calculations, transforming the often abstract and challenging concept of fractions into a practical, enjoyable exercise. The layered drinks not only serve as visual aids but also as tangible representations of mathematical principles.

Now, turning to potential questions:

1. Can you think of other mathematical concepts that could be effectively taught through food, similar to the approach described in the reading?
2.  How might these concepts be translated into a hands-on, enjoyable learning experience?

Andrea Hawksley (Bridges 2015) Exploring ratios and sequences with mathematically layered beverages

Top of Form

 

Activity

 

Reflection on Personal Exploration: 

Miura Ori Origami and Mathematically-Interesting Shoe Lacing

Embarking on the journey of trying out Miura Ori Origami and exploring mathematically interesting ways of lacing shoes has been a fascinating and eye-opening experience. Though seemingly unrelated, both activities offered a unique perspective on the interconnectedness of mathematics with everyday objects and artistic creations.

Miura Ori Origami: Unraveling Mathematical Beauty

Attempting the Miura Ori Origami technique, as demonstrated by Uyen Nguyen, was a delightful immersion into the world of mathematical elegance embedded in fashion design. The step-by-step video instructions (B) unveiled a mesmerizing sequence of folds that transformed a flat piece of paper into a three-dimensional masterpiece. The recurring patterns of triangles and parallelograms became apparent, showcasing the precision and symmetry inherent in the origami art form.

What struck me the most was the mathematical precision required to achieve the final result. The interconnected folds carefully considered angles, proportions, and geometric relationships. It was a reminder that even in the seemingly free-flowing world of art and design, mathematics plays a pivotal role in creating order and structure.

 

Shoe Lacing: Tying the Knot with Numbers

Shifting gears to the world of shoelaces, I delved into the Mathologer video, uncovering the intricate mathematics behind different lacing patterns. Before this exploration, I never thought much about the mathematical aspects of something as mundane as shoe laces. The video opened my eyes to the complexity and diversity of lacing techniques, each with its unique mathematical properties.

The revelation that the popular criss-cross and zig-zag lacing patterns are not just aesthetic choices but have mathematical underpinnings was intriguing. The emphasis on tight lacing and the connection to mathematical concepts, such as the contribution of each eyelet and the rapid increase in possibilities with more eyelets, showcased the intricate relationship between mathematics and seemingly unrelated daily activities.

In conclusion, both activities underscored the omnipresence of mathematics in our lives, whether in the meticulous folds of an origami creation or the efficient lacing of shoes. These experiences have heightened my appreciation for the beauty and functionality that mathematics brings to even the most ordinary aspects of our daily routines.

Questions to ponder:

1. Consider incorporating mathematical concepts into art forms or routine activities. How do you think this integration could enhance learning experiences and make mathematical ideas more accessible and engaging for a broader audience?

 

 

Miura Ori - Traditionelle Miura-Faltung

https://www.youtube.com/watch?app=desktop&v=EEGmnKKKhrk

What is the best way to lace your shoes? Dream proof.

https://www.youtube.com/watch?v=CSw3Wqoim5M

Week 7 Mathematics & poetry and novels

 

Reading

As I delved into the reading on Surfing the Möbius Band, a couple of significant 'stops' captured my attention, sparking a reflective journey into the intersection of art and mathematics.

The first 'stop' arises when the authors discuss the formal experiment in issue 11 of the Silver Surfer series, titled "The Moebius Madness of Silver Surfer." The decision by Dan Slott and Mike Allred to structure the storytelling using the form of a Möbius band is intriguing. The Möbius band, known for its representation of change and renewal, becomes a metaphor within the comic, symbolizing the cyclical nature of time and space in the Marvel universe. This integration of mathematical concepts into the narrative is a unique storytelling device and prompts a deeper reflection on the character's existential journey. The Möbius band becomes a visual cue, guiding readers through Silver Surfer's temporal loop and emphasizing the importance of free will in breaking the cycle.

Another 'stop' occurs when the reading explores the broader cultural impact of the Möbius band in fiction. The Möbius band, with its odd topological properties, has been utilized in various stories to symbolize either an endless loop or a mysterious transition to 'the other side.' Examples from Star Trek to an Argentinean film illustrate the diverse ways in which this mathematical figure has been woven into the fabric of storytelling. The reading suggests that the Möbius band, beyond its mathematical accuracy, holds a powerful place in the collective imagination, serving as a symbol for the unending and the cyclical in literature and art.

As I reflect on these 'stops,' I wonder how readers perceive the integration of mathematical concepts into the visual storytelling of comics. Does this enhance or detract from their engagement with the narrative?

In conclusion, the reading not only explores the creative use of mathematical concepts in comics but also raises questions about the accuracy of these representations. The fascinating interplay between art and mathematics in Silver Surfer's story prompts me to appreciate the beauty of their union while recognizing the occasional discrepancies that arise when mathematical symbols enter popular culture.

Activity

As I immersed myself in Sarah Glaz's introduction to the Fibonacci poems for Bridges 2021, a pivotal moment emerged in the creative process and collaborative spirit behind the collection.

Indeed, it is the origin story of the Fib poems within the Bridges poetry community. The virtual setting of the Bridges 2021 conference, designed as the town of Königsberg with its seven bridges, became the catalyst for the poetry gathering in the Glade. The challenge of limited time for over thirty poets led to the ingenious idea of blink-poems, specifically Fibs. This creative solution, sparked by Alice Major and refined through collaboration, not only facilitated a quick read-around but also paved the way for forming a unique collection. It highlights the adaptability and inventiveness that can arise when artistic minds come together to navigate challenges.

Another noteworthy 'stop' explains the Fibonacci sequence and how it translates into Fib poems. Glaz provides a concise and clear understanding of the mathematical underpinning of Fibs, tracing their syllable count back to the Fibonacci numbers. However, I struggle to complete my poems below and will continue the work when I feel more rested and inspired. This intersection of mathematics and poetry adds depth to the creative process, emphasizing the harmonious blend of two seemingly disparate disciplines. The structured nature of Fib poems, derived from the Fibonacci sequence, presents a fascinating framework for poets to explore and express their ideas.

Now, as I reflect on these 'stops,' I wonder how the poetic form derived from the Fibonacci sequence influences the thematic choices made by the poets. How do they navigate the constraints of the form to convey their ideas effectively?

Algebraic Equations

X

plus

Y makes Z

Solving for the unknown

?????????????????????

Geometric Points

Circles

spin

around points

??????????????????????

Explanation:

For the first Fib poem, "Algebraic Equations," I explored the realm of algebra and the process of solving equations. The Fibonacci sequence determined the syllable count in each line (1, 1, 2, 3, 5, 8), guiding the poem's structure.

In the second Fib poem, "Geometric Points," I delved into the world of geometry. The Fibonacci sequence dictated the syllable count in each line (1, 1, 2, 3, 5, 8), shaping the poem's progression. The lines aim to capture the elegance and precision of geometric shapes.

Poetry in the Glade: Bridges 2021 Fib CollectionTop of Form

 

Viewing

Exploring the diverse landscape of mathematical poetry through the lenses of various poets has been an enriching experience. With their unique background and perspective, each poet brings a distinctive flavor to the intersection of mathematics and art.

About my learning and wonders	About the Poets
Stephanie Strickland's "The infinity stops between our fingers." Strickland's work, marked by a lifetime achievement award, introduces me to the intriguing realm of digital literature. The poem suggests an exploration of the infinite within the finite, perhaps within the context of human connection. The use of digital media adds a layer of complexity, urging me to explore how technology amplifies the poetic narrative.	Website: https://en.wikipedia.org/wiki/Stephanie_Strickland Sample poem: The infinity stops between our fingers
Kaz Maslanka's "Hwadu" Maslanka's journey from a BFA in Sculpture to pioneering mathematical visual poetry fascinates me. “Enigmas are to Ontology as The Song of Ancient Dreams are to The Sound of the Ocean”. "Hwadu" not only highlights his artistic prowess but also brings me into a world where mathematical concepts transform into visual art. The connection between mathematics and poetry, elucidated through his work, prompts me to ponder the intricate beauty of numbers and aesthetics.	Website: http://mathematicalpoetry.blogspot.com/  Sample poem: Hwadu
Susan Gerofsky's "Glided, gilded and Barely, bleary." Gerofsky's commitment to a multidisciplinary approach is evident, blending mathematics, arts, and environmental education seamlessly. The poem, employing the constraints of a Fib and adding the layer of anagrams, creates a nuanced exploration of contrasting states. Using anagrams, like "Glided/gilded" and "canoe/ocean," adds an extra layer of complexity, reflecting the intertwining nature of mathematics and language. The choice to structure the twenty syllables into two iambic pentameters adds a rhythmic quality, echoing the cadence of a mathematical heartbeat. I wonder what sensory experiences might have inspired Gerofsky's exploration of contrasting states in this Fib poem.	Website: https://edcp.educ.ubc.ca/susan-gerofsky/ Sample poem: Glided, gilded and Barely, bleary
Dan May's "Eight Minutes" May's exploration of connections between mathematics and poetry within the teaching context offers a unique perspective. "Eight Minutes" sparks my interest in how he navigates the intersections of musicology, mathematics education, and poetry. The poem suggests a concise yet impactful exploration of a mathematical concept, leaving me intrigued about the depth within simplicity.	Website: https://talkingwriting.com/daniel-may-poem Sample poem: Eight minutes
Larry Lesser's "E(X)" As a distinguished teaching professor, Lesser's engagement in mathematical poetry and songwriting resonates with me. "E(X), the expected value, is the mean of all possible outcomes of a statistical experiment where each outcome is weighted by its probability." Indeed, it hints at a statistical exploration, and I am curious about how he weaves statistical concepts into poetic narratives. Also, his prolific presence in various literary and mathematical platforms prompts me to reflect on the broader impact of such interdisciplinary endeavors.	Website: https://larrylesser.com/poet-larry-ate/ Sample poem: E(X)

 

In delving into the works of these poets, I find myself on a journey where mathematical ideas intertwine with diverse artistic expressions. The poets' distinct styles and approaches invite further exploration into the multifaceted relationship between mathematics and poetry. How do these poets uniquely bridge the gap between mathematical precision and poetic expression? 

 Bridges Math and Art 2024 Virtual Poetry Reading website

 

Final Project Proposal: Tony Domina

 Here is the link

Outline Prosal Final Feb 12.docx - Google Docs

Week 6: Mathematics & dance, movement, drama and film

 This week's reading on mathematical learning through the reenactment of choreographed performance analyses of three cases in which groups of four (quartets) worked with video recordings of the 2016 Rio Olympic Games opening ceremony. Exploring how collaborative actions can foster mathematical understanding and artistic expression is fascinating. Two noteworthy "stops" in the text stand out for reflection.

First Stop: Integration of Physical Props and Collective Action: one critical aspect is emphasizing the physical engagement of quartets with the shiny plastic sheet, or Mylar, as a prop. Indeed, the quartets actively dissect and reenact movements, exploring the prop's physical possibilities. This collective manipulation of the prop becomes a medium for learning, creating geometric shapes and structures at various levels, from quartet to assembly to the entire performance. Also, integrating physical props adds a tactile dimension to the learning process, making it more immersive and engaging. The connection between physical actions and mathematical concepts, such as rotations, reflections, and translations, highlights the embodied nature of learning.

Second Stop: Ensemble Learning as a Coherent Unity: another significant aspect is the layered nature of ensemble learning, where the quartet, assembly, and whole performance levels interact dynamically. Indeed, the quartet level serves as a manageable entry point for participants, allowing them to enact critical aspects of the performance. This leads to exploring mid-level assemblies, creating geometric figures, and propagating waves. Finally, the highest-level performance unfolds with crystalline structures, liquid waves, and vortex motion. Therefore, the high level of coordination emphasizes the coherent integral unity of the performance. The quartet's engagement is not isolated; it contributes to the ensemble's significance and impact, showcasing the learning experience's collective nature.

Questions for further exploration include how physical prop interactions enhance mathematical understanding and the potential applications of this ensemble learning approach beyond dance and mathematics.

Questions for Discussion:

1. How does integrating physical props, such as the Mylar sheet, enhance the learning experience for the quartets? Can you think of other examples where tangible objects contribute to mathematical understanding?
2. In what ways does the layered structure of ensemble learning, from quartet to assembly to the whole performance, reflect the interconnectedness of mathematical concepts? How might this approach be applied to other disciplines beyond dance and mathematics?

Vogelstein, Brady, and Hall (2019) Reenacting mathematical concepts in large-scale dance performance

 

Reflection on the "Rope Polygons" Lesson:

The "Rope Polygons" lesson provides a unique and engaging approach to teaching geometry concepts, mainly focusing on measurement, reasoning with shapes, and understanding polygon properties. Indeed, I have not tried this activity. However, I would ask students to explore the properties of different polygons, such as triangles, quadrilaterals, pentagons, and hexagons. Using a twelve-foot knotted rope adds a kinesthetic and collaborative element to the learning process, making geometry come alive in a new context. The main task, challenging groups to create regular polygons with their bodies and the rope, is a hands-on and dynamic way to bridge the gap between abstract geometric concepts and real-world applications. Moreover, facilitating a whole-group conversation after the activity allows students to articulate their thought processes, share challenges, and learn from each other.

Also, I would suggest extensions for further exploration, such as investigating angle measures, side lengths, diagonals, and relationships between surface area and perimeter. This will allow for differentiation based on student readiness and interest. These extensions would encourage students to think beyond the initial challenge and deepen their understanding of geometry.

Moreover, I like allowing confusion and intervention when consensus cannot be reached. This pedagogical approach acknowledges the value of struggle in the learning process. It aligns with the idea that confusion can be a stepping stone to learning, fostering resilience and problem-solving skills. Finally, the reflective component, where students draw a picture to map out and showcase their group's approach to the challenge, is a valuable assessment tool. It reinforces their understanding and provides a visual representation of their learning journey.

http://www.malkerosenfeld.com/lesson-plans.html

Week 5: Developing mathematics pedagogies that integrate embodied, multisensory, outdoors and arts-based modalities

 Part 1: Reading

In this week's reading, two key points stand out to me. The first is the acknowledgment of the interconnectedness of physical movement, interaction, and mathematical learning. The article highlights the significance of opportunities for physical movement and expression in shaping how we think, learn, and communicate about mathematics. The notion that mathematical thinking cannot be separated from the settings in which it occurs resonates with me, emphasizing the dynamic relationship between the body, the environment, and mathematical activities.

The second remarkable 'stop' is the theoretical framing of the study, which brings together perspectives on the social production of learning spaces and embodied interaction. Theoretical frameworks often serve as guiding lenses, and in this case, combining ideas about the social spaces of learning with the importance of embodied action in mathematics education creates a rich foundation for understanding how whole-body collaboration can influence the spatiality of learning environments.

The research method involves pictures of learners participating in whole-body, multi-party activities, specifically focusing on walking scale number lines (WSNL) and whole and half (W + H). To illustrate, the WSNL participants incorporate classroom-based practices, using arithmetic computations on the gymnasium number line. In contrast, W + H participants perceive the activity as a departure from traditional methods, emphasizing the enjoyment of the embodied experience. This divergence prompts questions about the potential of transforming school mathematics through body-based design.

The study underscores the importance of considering the theory of place in understanding the embodied self within a total environment. At a socio-theoretic level, the research seeks to redefine embodiment in mathematics education by highlighting the interconnectedness of corporeality, inter-corporeality, and space. Recognizing the need to comprehend these complex relationships, the findings stress the significance of understanding the consequences and potential of expansive learning designs. Ultimately, the research advocates acknowledging the nuanced nature of embodied, emplaced, and interactive aspects in mathematical thinking and learning, opening up possibilities for creative leverage in the field.

Now, I find myself pondering how these theoretical considerations translate into practice.

1) How can educators integrate whole-body, multi-party activities to enhance mathematical learning experiences?

2) How do students perceive and engage with these activities?

3) How might students' understanding of mathematical concepts evolve through embodied interaction?

 

Part 2: Activity: I still wonder how to integrate this week's activity into my teaching!

Week 4: Mathematics and the Arts Reflection on the Bridges Conference Reading

 

I delved into the vibrant and interdisciplinary realm of the Bridges Conference. Three distinct stops in the text caught my attention, each offering a unique perspective on the convergence of mathematics and art.

Stop 1: The Mathematical Garden and Polyhedral Climbing Structure (Fig. 1)

The Mathematical Garden, with its interactive features like puzzles, mazes, and a giant xylophone, is a testament to the immersive nature of the Bridges Conference. The polyhedral climbing structure, depicted in Fig. 1, not only symbolizes the interconnectedness of mathematical concepts but also exemplifies the playful integration of math into physical experiences. As a participant, I can only imagine the joy and intellectual stimulation of engaging in such a creative and educational environment. How does incorporating interactive installations in the Mathematical Garden enhance the conference experience for attendees?

 

Stop 2: Marjorie Rice's Pentagonal Tilings (Fig. 2)

 

Fig. 2 showcases a pentagonal tessellation on the ramp leading to the museum's entrance, setting the stage for the Reza Sarhangi Memorial Lecture. Marjorie Rice's story, a self-taught mathematician passionate about pentagonal tilings, is inspiring and intriguing. This episode highlights mathematical discovery's democratization and emphasizes the mathematical community's collaborative spirit. The use of unconventional notation and Marjorie's journey in discovering new pentagonal tilings sparks curiosity. How does Marjorie Rice's story contribute to reshaping the narrative around who can be a mathematician? In what ways do unconventional approaches to notation impact the exploration of mathematical concepts?

 

Stop 3: Hedy Hempe's "H-spiral" (Fig. 5)

 

Fig. 5 introduces us to Hedy Hempe's "H-spiral," an artwork crafted from carefully arranged eggshells, earning an Honorable Mention for 3-dimensional Artwork. As embodied in this piece, the fusion of mathematical concepts and artistic expression prompts contemplation on the diverse forms through which mathematical ideas can be communicated. How does the "H-spiral" exemplify the intersection of art and mathematics? In what ways does the inclusion of 3-dimensional artwork contribute to the broader narrative of the Bridges Conference?

In conclusion, this week’s reading has been a profound eye-opener for me, reshaping my perspective on the interconnected worlds of mathematics and art. Reflecting on the Mathematical Garden, Marjorie Rice's Pentagonal Tilings, and Hedy Hempe's "H-spiral," I am inspired by the seamless convergence of these disciplines at the Bridges Conference.

This newfound awareness extends beyond the conference walls. Last night, as I dined at a restaurant, I could not help but see the art in the subtle play of light, noticing the elegance of a sphere shape. It has become clear that exploring mathematical concepts is not confined to academic settings but extends into our daily experiences.

This realization prompts me to ponder: How do these seemingly ordinary encounters with mathematical aesthetics in our surroundings contribute to a broader appreciation of the intersection between mathematics and art?

Eve Torrance (2019), Bridges 2018, Nexus Journal

 Picture from the restaurant in North Vancouver

This week's activity:

Engaging with the Bridges Math Art Gallery, I explored a captivating Möbius band carved in Somerset Alabaster.

https://gallery.bridgesmathart.org/exhibitions/2011-bridges-conference/nickdurnan

 

While appreciating the accessible mathematics behind the piece, I ventured to understand its intricacies, striking a balance between familiarity and pushing my boundaries.

 The YouTube video on cutting Möbius strips provided additional insights, making the mathematical aspects more tangible and intriguing.

Why is cutting a Möbius strip so weird?

 https://www.youtube.com/watch?v=Qy0FSfEPBic

 I tried and got this:

Week 3: Sustainable mathematics in and with the living world outdoors

 

Reading Portion:

In this week's reading, Doolittle's exploration of the failures of the grid and its implications on spatial and temporal organization, three stops along this intellectual journey stand out and spark curiosity.

First Stop: Seductive Simplicity of the Grid

The journey begins with the seductively simple nature of the grid. This system effortlessly extends into domains like neighborhoods and towns and three-dimensional spaces like buildings and malls. Doolittle's analogy of gardening leading to geometry and the connection between linen and line resonates deeply. With its straight lines and right angles, the grid provides a sense of control, predictability, and mastery. However, the simplicity that makes the grid appealing also raises critical questions about its adaptability to the complexities of real-world applications. The tension in the fiber, which creates linearity, becomes a metaphor for the tension between imposed order and the organic growth and diversity of specific places.

Second Stop: Failures and Control

As the grid exploration progresses, Doolittle astutely observes that failures in the grid system have been apparent since its inception. However, responding to these failures raises essential questions about control and ownership. The grid, deeply ingrained in our thinking, leads to rules governing behavior, shaping our sense of control. The failure to let go of the grid results in the subordination of a place's unique qualities to the grid geometry's imposed uniformity. The grid is not merely a geometric construct but a manifestation of cultural and human tendencies toward order and control.

Third Stop: Giving Thanks and Liberation from the Grid

A fascinating turn in the journey comes with the Indigenous perspective, introducing the idea of giving thanks and offering an alternative solution to the Königsberg Bridges problem. Acknowledging what has been missing from the discussion, recognizing the river as a foundation, and giving thanks through offerings present a profound departure from the rigid confines of the grid. The narrative weaves through philosophy, bringing in Immanuel Kant and his habitual walks, drawing parallels to the mental abstraction imposed by accepting Euler's negative result. The call to widen our perspective, move off the grid, and see the world as it truly is bringing a refreshing perspective to mathematical problem-solving.

Engaging Questions for Reflection:

1. How do the failures of the grid, as highlighted by Doolittle, resonate with your understanding of spatial and temporal organization in various contexts?
2. How can alternative geometries, described as "geometries of liberation," find a place in modern mathematics education, and what challenges might arise in incorporating them into the classroom?

Reference:

Doolittle, E. (2018). Off the grid. In Gerofsky, S. (Ed.), Geometries of liberation. Palgrave. https://doi.org/10.1007/978-3-319-72523-9_7

 

Activity Portion:

My son's drawing                                                               My spouse's drawing.

The activity described in Doolittle's "Off the Grid" gave me a unique perspective on observing and sketching the world around me, even if I could not go outdoors. I was sitting indoors with my spouse and two-and-a-half-year-old son. We looked through the window; we focused on living beings and human-made things, using watercolors and brushes to document my observations. I did the observation, and my spouse and son made the drawings. As I found a spot to sit and observe, I noticed various lines and angles in the natural and human-made things. I observed natural flowing lines like plants, trees, rocks, and the sky. The natural world seemed to express itself through gentle curves and irregular shapes. On the other hand, human-made things, like buildings, roads, fences, and street lights, displayed more structured and geometric lines and angles. Therefore, the contrast between the organic and the structured was apparent.

Reflecting on these observations, it became evident that specific patterns emerged in both living and human-made elements. While living things displayed a sense of irregularity, human-made objects adhered to a more ordered and intentional design. However, there were exceptions, as nature sometimes exhibited symmetrical patterns, and human-made structures occasionally embraced organic forms. The patterns I observed raised questions about why such distinctions exist. I pondered whether these patterns are inherent like things or influenced by human perception and design choices. The contrast in lines and angles reflects a fundamental difference in the creation processes, one guided by nature and the other by human intention.

Considering how this activity could be translated into teaching, close observation, and sketching could be powerful tools for helping students understand lines and angles. By encouraging students to explore the world around them through drawing, educators can foster a deeper connection between their eyes and hands, promoting a more intimate understanding of geometry in their surroundings.

Moreover, I contemplated integrating whole-body movement into the learning experience. For instance, the video of two UBC undergraduate students, Sam Milner and Carolina Azul Duque, demonstrates the  Dancing Euclidean Proofs. Indeed, it suggests one-way students could experience lines and angles through activities that involve exploring the outdoors. I wonder what other ways we can engage students with the living world to offer a holistic understanding of geometry, connecting abstract concepts to tangible, real-world experiences. This approach could make learning more immersive and memorable for students.