Trigonometry Flex your Muscle!

https://drive.google.com/drive/folders/17xOE9b-lJ570lQXz-EaWosB8e8Qzjw9o?usp=drive_link

Final Project Draft

 https://docs.google.com/document/d/1IFJ5MoBbvcAfM7Sa-2tdfIwXnK2VH7h_/edit?usp=drive_link&ouid=104323376055760014489&rtpof=true&sd=true

Week 9: Mathematics & traditional and contemporary practices of making and doing

Reading 

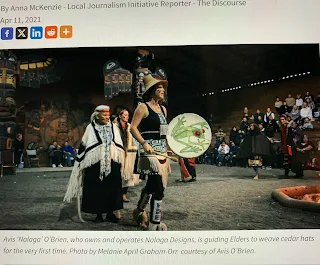
As I reflect on Avis O’Brien’s captivating journey, a Haida and Kwakwa̱ka̱ʼwakw woman weaving her way back to her cultural roots through cedar, I am struck by two significant stops in her transformative narrative.

First Stop: Reconnecting through Cedar Medicine

The initial turning point for O’Brien was in 2010 when she embraced the art of cedar weaving under the guidance of her sister, Meghann O’Brien. Before this, O’Brien harbored a sense of disconnection and shame about her identity, a product of historical impacts on Indigenous cultures. The power of cedar, described as sacred medicine, became the key that unlocked the door to her cultural heritage. This moment stands out as a powerful testament to the healing potential embedded within indigenous practices. O’Brien's experience underscores the idea that cultural reclamation can be a profound path to self-discovery and reconnection.

Second Stop: Weaving as Cultural Resilience

The historical context woven into O’Brien’s narrative reveals the deliberate suppression of Indigenous cultural practices by the Canadian government. The ban on Potlatches, a central element of First Nations' cultural and economic identity, exemplifies a systematic effort to erase indigenous cultures. As one of these suppressed practices, Weaving slept through those challenging times, but O’Brien sees its reawakening as an act of resilience. By facilitating cedar weaving workshops, she actively supports Elders in reclaiming what was taken from them throughout history. This stop on O’Brien’s journey highlights the enduring strength of Indigenous cultures and the power of individuals like her in revitalizing and preserving these traditions.

Question for Discussion:

1. In what ways does the intersection of cultural practices, such as cedar weaving, contribute to intergenerational healing and the preservation of Indigenous identity?

APTN article, Apr 11, 2021: ‘The spirit of the medicine will lead us back’: How Avis O’Brien is guiding Elders to weave their first cedar hats

Activity

This week's handmade rope-making exploration has been a delightful revelation, expanding my perspective on the mathematics embedded in a seemingly simple craft. As someone who frequently uses ropes but never considered their potential for teaching mathematics, this experience was an eye-opener. Engaging in the tactile process of creating 2-ply twine with two scarves felt like an intimate connection to a timeless human tradition, even though I quickly made the S twist and struggled with the Z twist. Sharon Kellis's insightful mention in the video of the possibility of creating a rope with anything. Also, she made the connection between rope making and the foundation of the new technology, as iPads added an extra layer of fascination to this age-old craft. Physically manipulating materials brought a profound sense of connection to our ancestors, instilling in me a grounding experience that resonates with the present.

When I made the S shape, I explored the mathematical patterning woven into each twist and turn of the scarves. It was a fascinating journey into the hidden complexities of the craft. As I twisted away from me, I marveled at the symmetry and uniformity of the resulting rope – all manifesting mathematical principles. The tension in my hands hinted at the possibility of exploring concepts like symmetry, geometry, and basic algebraic relations. It is intriguing how making rope can unveil a world of mathematical beauty, creating a bridge between the tactile and the abstract.

Indeed, handmade rope-making can be integrated into the curriculum, which opens doors to many enriching possibilities. Weaving the historical and cultural context of rope-making into lessons serves as a bridge, connecting ancient practices with contemporary mathematical understanding. For instance, students can be introduced to the mathematical concepts of symmetry, geometry, and algebraic relations through hands-on activities that bring these principles to life and engage students in a multisensory learning experience. Emphasizing the tactile sensation of rope making, the visual observation of patterns, and the kinesthetic experience of twisting creates holistic learning styles, making mathematical concepts more accessible and engaging.

In summary, handmade rope-making emerges as a powerful interdisciplinary tool, seamlessly weaving together history, culture, and mathematics. As educators, incorporating this craft into our teaching practices provides students with a unique and immersive learning experience, fostering a deep appreciation for the mathematical principles at play and the cultural significance of traditional crafts. As I reflect on this exploration, I am left wondering what unique perspectives students might bring to this age-old craft and how it could become a gateway for them to appreciate the mathematical and cultural significance of hands-on learning.

Top of Form

 

1) The art and geometry of rope making and yarn plying

2) Weaving the Bridge at Q’eswachaka

 

Week 8: Mathematics & fibre arts, fashion arts and culinary arts

 

Reflection on the Reading:

Exploring Ratios and Sequences with Mathematically Layered Beverages by Andrea Johanna Hawksley

As I delved into Andrea Johanna Hawksley's exploration of teaching ratios and sequences through layered beverages, I was captivated by the innovative approach to blending math with culinary delight. Two prominent stops in this reading stood out to me, offering unique insights into the intersection of mathematics and food.

The first notable stop is the introduction of simple two-layered beverages, a clever tool to enhance comfort with fractions and ratios. The author seamlessly integrates mathematics into cooking, highlighting the strict ratios in recipes and emphasizing the importance of understanding fractions. The example of expressing sweetness as a ratio between layers—3:5, for instance—creates a tangible link between the abstract world of numbers and the delicious experience of consuming layered drinks.

The second stop takes me into exploring sequences using beverages with many layers. The limitation that each layer must be less dense than the previous one narrows down the feasible sequences, introducing a fascinating challenge. The author introduces sequences like the Fibonacci sequence, demonstrating how the layers' proportions can mirror the sequence's mathematical properties. Creating a Fibonacci lemonade, where the intensity of flavors increases exponentially, adds a delightful twist to the exploration.

These stops underscore the dynamic relationship between mathematics and the sensory experience of consuming layered beverages. The interactive nature of the workshop engages participants in hands-on calculations, transforming the often abstract and challenging concept of fractions into a practical, enjoyable exercise. The layered drinks not only serve as visual aids but also as tangible representations of mathematical principles.

Now, turning to potential questions:

1. Can you think of other mathematical concepts that could be effectively taught through food, similar to the approach described in the reading?
2.  How might these concepts be translated into a hands-on, enjoyable learning experience?

Andrea Hawksley (Bridges 2015) Exploring ratios and sequences with mathematically layered beverages

Top of Form

 

Activity

 

Reflection on Personal Exploration: 

Miura Ori Origami and Mathematically-Interesting Shoe Lacing

Embarking on the journey of trying out Miura Ori Origami and exploring mathematically interesting ways of lacing shoes has been a fascinating and eye-opening experience. Though seemingly unrelated, both activities offered a unique perspective on the interconnectedness of mathematics with everyday objects and artistic creations.

Miura Ori Origami: Unraveling Mathematical Beauty

Attempting the Miura Ori Origami technique, as demonstrated by Uyen Nguyen, was a delightful immersion into the world of mathematical elegance embedded in fashion design. The step-by-step video instructions (B) unveiled a mesmerizing sequence of folds that transformed a flat piece of paper into a three-dimensional masterpiece. The recurring patterns of triangles and parallelograms became apparent, showcasing the precision and symmetry inherent in the origami art form.

What struck me the most was the mathematical precision required to achieve the final result. The interconnected folds carefully considered angles, proportions, and geometric relationships. It was a reminder that even in the seemingly free-flowing world of art and design, mathematics plays a pivotal role in creating order and structure.

 

Shoe Lacing: Tying the Knot with Numbers

Shifting gears to the world of shoelaces, I delved into the Mathologer video, uncovering the intricate mathematics behind different lacing patterns. Before this exploration, I never thought much about the mathematical aspects of something as mundane as shoe laces. The video opened my eyes to the complexity and diversity of lacing techniques, each with its unique mathematical properties.

The revelation that the popular criss-cross and zig-zag lacing patterns are not just aesthetic choices but have mathematical underpinnings was intriguing. The emphasis on tight lacing and the connection to mathematical concepts, such as the contribution of each eyelet and the rapid increase in possibilities with more eyelets, showcased the intricate relationship between mathematics and seemingly unrelated daily activities.

In conclusion, both activities underscored the omnipresence of mathematics in our lives, whether in the meticulous folds of an origami creation or the efficient lacing of shoes. These experiences have heightened my appreciation for the beauty and functionality that mathematics brings to even the most ordinary aspects of our daily routines.

Questions to ponder:

1. Consider incorporating mathematical concepts into art forms or routine activities. How do you think this integration could enhance learning experiences and make mathematical ideas more accessible and engaging for a broader audience?

 

 

Miura Ori - Traditionelle Miura-Faltung

https://www.youtube.com/watch?app=desktop&v=EEGmnKKKhrk

What is the best way to lace your shoes? Dream proof.

https://www.youtube.com/watch?v=CSw3Wqoim5M